多邊形

多邊形定義為各點互相直線連接所圍成的無開口圖形。
多邊形又包含以下幾個種類：

• Simple Polygon 簡單多邊形
• Convex Polygon 凸多邊形
• Concave Polygon 凹多邊形

簡單多邊形

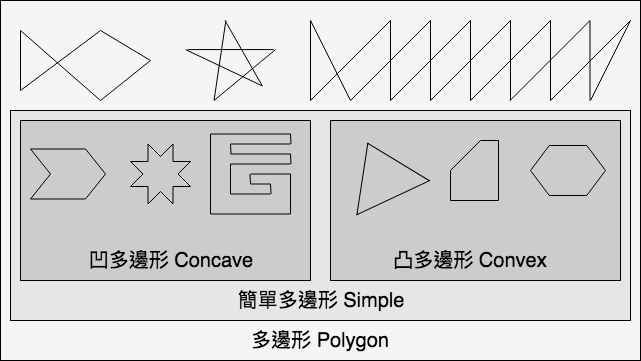
簡單多邊形必須符合多邊形條件且任何一邊都沒有交叉。
但如何以N點建造一個簡單多邊形並且確定任何一邊都沒有交叉？

Naïve Method 樸素法

簡單方法利用點列表的順序連接各點，在與最後一點與第一點連接完成多邊形。
因為這種方法是隨機依照列表順序(任何一種列表)連接各點，因此畫出來的圖形並無絕對。
下圖為兩種成功畫出簡單多邊形的例子。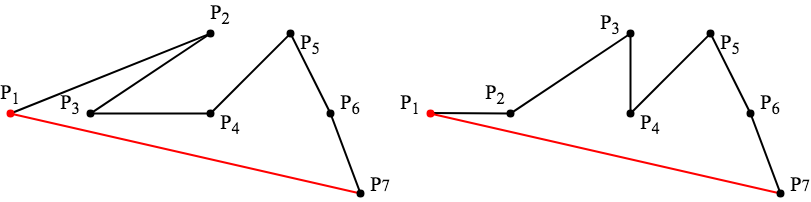

結論

這種方法在大多數例子都無法成功畫出簡單多邊形，因為這種方法沒有一定的點對點連接順序。
下圖為非簡單多邊形的例子。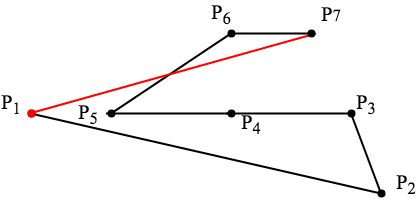

Circular Scan 圓型掃描

圓型掃描是在所有點中選擇一個中心點進行掃描，每次掃描到得點加入列表中，如果同一條線上兩個以上的點，則以離中心點最近的優先加入列表。
雖然隨機選擇中心點有可能成功建立簡單多邊形，但也可能錯誤選擇中心點。
下圖為隨機選擇一點(非從點列表中選擇)為中心點的例子。

如果加以分析，會發現隨機選擇一點為中心點，還是會無法讓第一點及最後一點正確連接。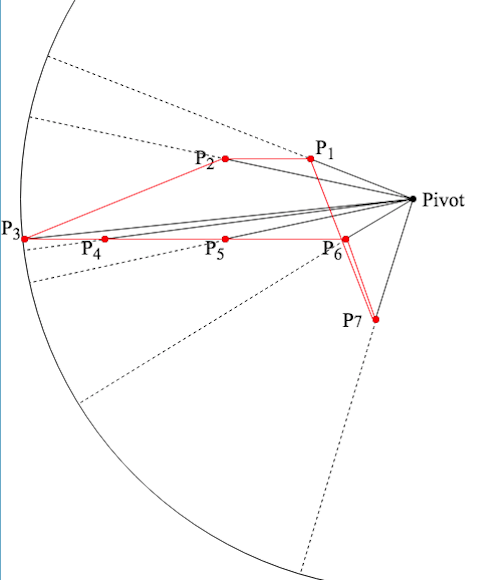

為了避免第一點及最後一點錯誤連接，中心點必須選擇點列表的一點。
但是隨機選擇，還是無法確保所建立的多邊形為簡單多邊形。
因此，可以選擇在最大或最小X值的點或是在最大或最小Y值的點。
下圖為選擇最大X值的點。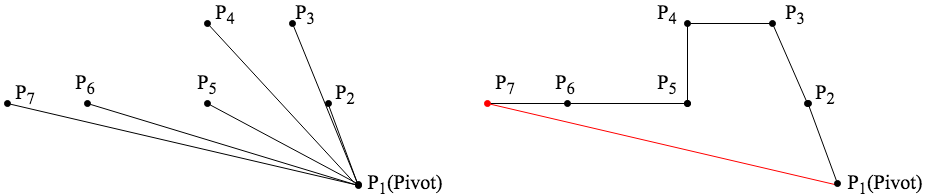

以中心點加以分析會發現，第一點及最後一點所延伸到圓的直線，會是扇形的兩邊。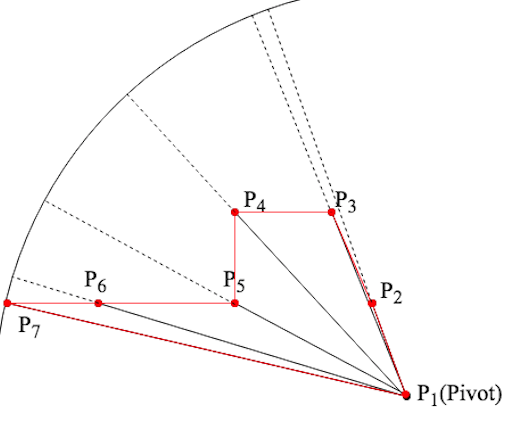

結論

如果隨機選擇中心點或是點列表中隨機一點，都無法確保所建立的多邊形為簡單多邊形。
但是選擇在最大或最小X值的點或是在最大或最小Y值的點，可以改善並建立簡單多邊形

傳送門：[筆記本: 演算法] 多邊形篇 Part 2 - Convex Hull 凸包
傳送門：[筆記本: 演算法] 多邊形篇 Part 3 - Furthest Pair of Points 最遠兩點配對